Summary of Studies of the General Circulation of the Atmosphere with a Simplified Moist General Circulation Model, my PhD thesis.
 Primary arguments:
Primary arguments:
- Development, testing, and experiments with a simplified moist GCM.
Discussion:
My thesis consists of slightly longer versions of the following papers (mostly with
just longer introduction and conclusion sections): the Frierson, Held
and Zurita-Gotor papers on static stability and eddy
scale and energy fluxes in midlatitudes, the
Frierson 2007 paper on convection schemes, and the
Frierson, Majda and Pauluis precipitation fronts paper.
There's also a more
complete description of the simplified moist GCM, in particular with more
detail on the gray radiation scheme (including radiative equilibrium
calculations), a full description of Monin-Obukhov theory, and a complete
nondimensionalization of the GCM and other similar simplified GCMs such as
the Held-Suarez model.
The complete nondimensionalization of the model (which was quite tedious to
perform) was
motivated by our studies on a "hypohydrostatic" model (see the
Pauluis et al and Garner
et al
papers for more detail on this). We were looking for a way to tell when
different parameter variation experiments with the model are isomorphic
(e.g., is varying the planetary radius equivalent to varying the depth
of the atmosphere in this GCM, as both change the aspect ratio?
Can they be equivalent if other model parameters are also
varied?). We ultimately came to the conclusion that performing such a
nondimensionalization is the only way to provide mathematical proof
that two parameter experiments are identical. Check out Section 2.8 of
the thesis for more detail on the nondimensionalization of GCMs.
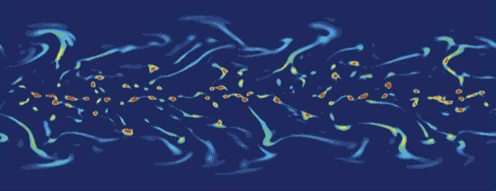
The figure above is an instantaneous precipitation distribution for a
control simulation with the simplified moist general circulation model.
Full citation:
Frierson, D. M. W. Studies of the General Circulation of the Atmosphere
with a Simplified Moist General Circulation Model. Ph.D. thesis, Princeton
University, 218 pp, 2005.
A PDF download of the full thesis can be found here.
|
|