Summary of Large Scale Dynamics of Precipitation Fronts in the Tropical Atmosphere: A
Novel Relaxation Limit by Frierson, Majda and Pauluis, which appears in Communications in Mathematical Sciences.
 Primary arguments:
Primary arguments:
- Exact solutions for the movement of "precipitation fronts": the interfaces
between dry and moist regions in the tropics.
-
Study of conservation laws, which demonstrate that discontinuities in
vertical velocity and precipitation can
develop in finite time, and proof in a steady Walker cell.
Discussion:
For
my general examination project at Princeton, Isaac and I worked on a
simple model of the tropics, with a two-layer atmosphere with moisture
and a dynamical ocean, to study ENSO dynamics in a simple setting.
While we didn't continue the ENSO work, I hooked up with Andy and
Olivier, who each had ideas about how you can solve the
atmospheric equations fully in some new circumstances, involving the
motion of the boundary between moist and dry (precipitating and
non-precipitating) regions.
Condensation is fundamentally a nonlinear process, but it's an unusual
(and somewhat tractable) nonlinearity. When a parcel of air is
subsaturated, no condensation occurs. When a
parcel becomes saturated, condensation occurs in the exact
amount to keep the parcel at saturation (I'm ignoring any complex
microphysics with this statement). This sort of nonlinearity is
actually quite simple in some ways, especially in the context of the
linearized two-layer dynamics that we study in this paper: it means
that in the dry regions of the model, the equations are completely
linear (with dry gravity waves governing the dynamics), and in the
moist regions, the equations are linear as well (with moist gravity
waves determining the dynamics). The nonlinearity only comes in through
the movement of the interface separating dry and moist regions. We
develop a method that determines the speed of this interface given the
characteristics in the surrounding moist and dry regions.
In this paper, we also examine some conservation laws, which we use to show
that discontinuities in precipitation can develop in finite time in the
model. The estimates that we construct show why (and under what conditions)
simulations with the QTCM and other
similar simplified models of the tropics develop discontinuities/sharp
structures in precipitation, vertical velocity, and other first derivative
quantities. An analogous discontinuity in precipitation can be seen in
Walker cell simulations with the QTCM by Bretherton and Sobel (2002, JAS).
We have continued this work in a submitted manuscript (Pauluis, Frierson and Majda),
in which we study some related properties of this system. A
particularly interesting result is that reflection of perturbations can
occur at precipitation fronts, because these mark the boundary between
dry regions which have fast wave speeds, and moist regions
which have slow wave speeds. We construct analytic solutions for
the reflection and transmission coefficients in that paper.
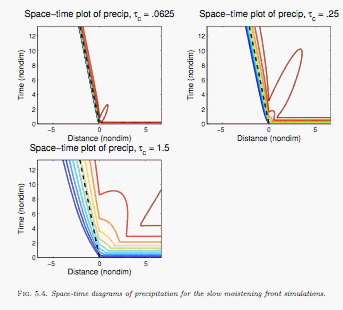
The figure above compares simulations of precipitation fronts with
different finite relaxation times with theoretical predictions from the
infinitesimal limit. The theoretical predictions work well
even for realistic convective relaxation times. This work has
been extended by Stechmann and Majda, who developed a theory for the structure of these fronts at finite convective relaxation times.
Full citation:
Frierson, D. M. W., Majda, A. J. and O. M. Pauluis. Large Scale Dynamics of
Precipitation Fronts in the Tropical Atmosphere: A Novel Relaxation Limit.
Communications in Mathematical Sciences, 2, 605-640, 2004.
The official journal link can be found here.
A PDF download of the full paper can be found here.
This download is courtesy of the International Press of Boston, who owns sole
rights to it. The download is subject to copyright laws and statutes. For more
information, please visit the International Press website.
|
|