Summary of A Gray-Radiation Aquaplanet Moist GCM. Part I: Static Stability and Eddy
Scales by Frierson, Held and Zurita-Gotor, which appears in Journal of
the Atmospheric Sciences.
 Primary arguments:
Primary arguments:
- Development of a simplified moist general circulation model for studies
of large scale dynamics.
- Midlatitude static stability is controlled by moisture over a wide range
of parameters.
- Length scales vary remarkably little despite large changes in static
stability.
Discussion:
Our first goal with this work was to design a simplified moist general
circulation model, something along the lines of the Held-Suarez dry GCM, but with moisture. In particular, we wanted a model in which
we could vary the atmospheric moisture content over a wide range, to get an
idea of how the midlatitude jet stream, pole-to-equator temperature gradients,
the Hadley circulation, the location of rainy and dry regions, etc., are
influenced by latent heating.
We chose idealized physical parameterizations
for the model, which allow for ease of interpretation of results and reproducibility. Since we
wanted to design an energetically consistent system, the model ends up being
quite a bit more complicated than the Held-Suarez model, but still is
significantly simpler than a full GCM. You can read the paper for specifics
on what we chose and why, but I'll highlight here a few of the choices that
seem to surprising or confusing to people.
First, often people are surprised to see that the model can be run without
a convection scheme, i.e., with grid scale condensation only (we referred to
this as "large scale condensation only" in the paper, but "grid scale
condensation only" is a better term. See the description of Frierson 2007a
for reasons why). One might think that running with grid scale condensation
only might cause the model to blow up, since the strong radiative heating
near the surface creates strong convective instability, which goes to the
smallest scale unless a convection scheme is present (see also
Garner et al 2007). However, the model can indeed run despite the strong
instability.
In retrospect, one part of the model that we probably should have simplified
is the stable side of the drag coefficient and boundary layer
parameterization. When the surface is stable, we reduce the drag
coefficients and the corresponding boundary layer diffusivities according to
Eqns. 11 and 18. However, in the simulations here, the surface is rarely in
a stable state, and when the surface is stable, the reduction in drag
coefficient is minimal. Therefore, those wishing to reproduce these
calculations should be able to do so in a simpler manner by using the
unstable drag coefficient and boundary layer parameterization (Eqns. 12 and
19) in all cases. Stable surface layers would be important for instance over
high latitude land surfaces in the winter, so the model as described is more
easily extended to cases with land.
One of the first things that one notices when changing the moisture content
in this model is how easy it is to change the isentropic slope in
midlatitudes: the midlatitude static stability increases greatly with
moisture content. Typical theories for static stability/isentropic slope
(Stone 1972, Held 1978, Schneider 2004) are based on dry baroclinic eddy
dynamics, and do not predict such changes in static stability. I have
investigated midlatitude static stability in two other papers, Frierson 2007c
and Frierson 2006.
With a large change in midlatitude static stability, one might expect a
large change in baroclinic eddy length scales, since these are often thought
to be determined by the Rossby radius of deformation. However, we see
no such change in eddy length scales in the midlatitudes, which stay
remarkably fixed in these simulations. We instead interpret the change in
terms of the Rhines scale, which may indicate that a turbulent cascade may
be present in our simulations. The question of what determines baroclinic
eddy length scales in the presence of moisture is one I am actively
investigating with Ed Gerber and Lorenzo Polvani.
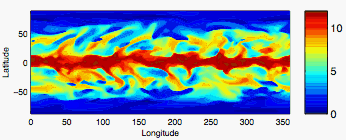
The figure above is an instantaneous plot of the boundary layer depth
in the dry limit simulation we study here. This plot is key to
showing that convection reaches the tropopause well into the
midlatitudes in this simulation.
Full citation:
Frierson, D. M. W., Held, I. M. and P. Zurita-Gotor. A Gray-Radiation
Aquaplanet Moist GCM. Part I: Static Stability and Eddy Scales. Journal
of the Atmospheric Sciences, 63, 2548-2566, 2006.
The official journal link can be found here.
A PDF download of the full paper can be found here.
This download is courtesy of the AMS, who owns sole rights to it.
The download is subject to copyright laws and statutes. For more
information, please visit the AMS/Allen Press website.
|
|